Далеко ли до Луны? Рациональные диапазоны роста биткойна

Bitcoin-Novosti.ru

«Как быстро биткойн будет расти дальше?» – должно быть, главный вопрос для большинства криптоинвесторов. Каждый день множество людей пытаются дать на него ответ, но высокая волатильность биткойна и циклы хайпа делают такие точечные прогнозы практически бесполезными. Однако методами стандартной регрессии, учитывающей неопределённость в ценовой динамике биткойна, можно спрогнозировать диапазон ценовых значений, у которого будет гораздо больше шансов на то, чтобы совпасть с реальностью. В этой статье я привнесу простое, но эффективное, изменение в используемую обычно степенную модель и попробую с помощью получившейся модели спрогнозировать несколько диапазонов вероятных значений – для даты достижения ценой биткойна ключевых уровней и среднегодовой доходности. Результаты могут быть информативными и полезными для принятия инвестиционных решений.

Методы

Модель цены

История цены биткойна насчитывает уже около 10 лет. 3319 суточных точек данных в моём источнике (файл .csv) – этого более чем достаточно для применения базового математического моделирования, и выбор доступных ценовых моделей велик. Здесь я упомяну две из них:

  1. Превосходная модель на основе дефицитности (определяемой по отношению запасов к приросту) от PlanB
  2. Модели DaveTheWave (англ.), основанные на двухпараметрической логарифмической регрессии

Хотя между моделями этих двух авторов есть принципиальные различия, в обеих для массива вводных данных применяется следующее уравнение:

или, в иной записи:

A и B в этих уравнениях являются константами, определяя линейную функцию между log (x) и log (y), и получаются путём минимизации наименьших суммированных квадратов расстояний между моделью и реализованными наблюдениями. Линейная зависимость между логарифмами двух сущностей – это свойство закона степенной зависимости. Степенные зависимости в ценовых моделях для биткойна фундаментально имеют абсолютный смысл, как PlanB чётко объяснил и продемонстрировал исходя из постепенно возрастающего дефицита биткойна.

Добавление параметра сдвига по времени

Хотя мои первые пробы вполне удовлетворительно реконструировали опубликованные диаграммы вышеназванных моделей, и я мог остановиться на этом, мне удалось улучшить подгонку, добавив в уравнение третий параметр S:

или, в иной записи:

Параметр A – это наклон линии между log(x+S) и log(y), B – это точка пересечения этой линии (пересечение оси Y), а S отвечает за точку сингулярности входной логарифмической функции. S сдвигает точку начала отсчёта, так что вместо предположения о том, что первые доступные данные о цене совпадают с началом отсчёта, или что начало отсчёта совпадает с генезисным блоком Биткойна, мы предоставляем модели возможность самостоятельно определить начало отсчёта.

Метод подгонки

При использовании двухпараметрической степенной модели достаточно выполнить линейную подгонку между log(цена) и log(время). С введением третьего параметра возникает необходимость использования нелинейного метода подгонки. Её можно выполнить с помощью алгоритма Левенберга — Марквардта, применимым с любыми параметрическими нелинейными уравнениями. Я использовал для этого платформу LabVIEW, но это же можно сделать и на других платформах.

Результаты

Подгонка

Уравнение, в котором y = цена биткойна на конец 1 сентября 2019 г., а x = количество дней от самой ранней точки в исторических ценовых данных биткойна (17 июля 2010 г.), будет выглядеть так:

или, в иной записи:

R² (коэффициент детерминации) равен 0,935, что означает, что сглаженная кривая, определённая тремя параметрами, составляет 93,5% от общей дисперсии в истории цены биткойна. Неплохо. На графике ниже эта подгонка показана зелёной линией (шкала времени линейная, цены – логарифмическая).

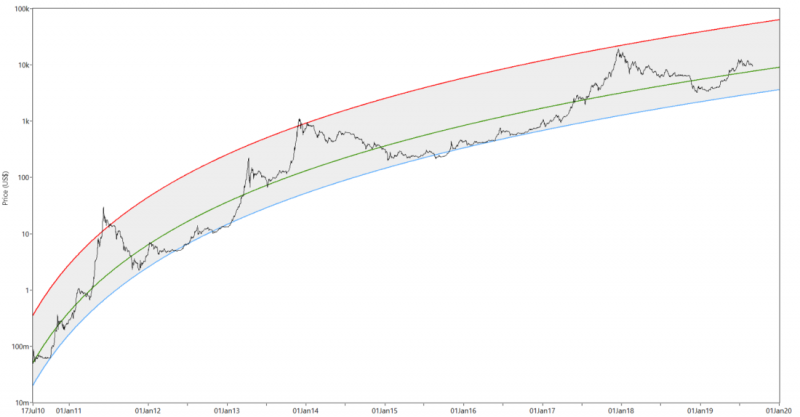
Далеко ли до Луны? Рациональные диапазоны роста биткойна

Алгоритм Левенберга — Марквардта использовался для подгонки трёхпараметрической кривой степенной зависимости к дневной цене биткойна (чёрная линия) с 17 июля 2010 г. до 28 августа 2019 г. (зелёная линия). Чтобы получить интервал, исходя из которого можно будет оценить диапазон значений, я взял коэффициент 7x (красная кривая) и 0,4x (синяя кривая) от цены зелёной линии.

Обратите внимание, что 10^(-13,43) – число небольшое, а (x+312)^4,860 – переменное по времени большое число. Перемножением этих чисел достигается магия создания зелёной линии выше. Давайте убедимся в работоспособности модели, применив эту формулу к значениям 2 сентября 2019 г., через 3334 дня после 17 июля 2010 г., нашей первой точки данных о цене биткойна:

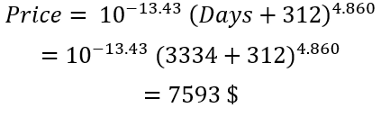
Далеко ли до Луны? Рациональные диапазоны роста биткойна

Это цена модели для 2 сентября. Фактическая цена на конец дня составила 9941,97 $ (источник). Таким образом, согласно модели, биткойн на тот момент был переоценён на 31%. Для биткойна в этом нет ничего особенного.

Расчётный временной диапазон

Убедившись, что модель удовлетворительно и правдоподобно соответствует изменениям цены биткойна с течением времени, я перешёл к настройке интервала вокруг цены модели, настолько широкого, насколько это будет необходимо, чтобы он включал в себя максимумы и минимумы на протяжении всей доступной истории цены биткойна. Попробовав для этого несколько методов, я заметил, что ценовые максимумы биткойна раз за разом формировались на уровне, примерно в 7 раз превышающем смоделированную цену (красная линия на графике выше), а минимумы – примерно в 0,4 раза ниже смоделированной цены (синяя линия). Использовав 7 и 0,4 в качестве постоянных коэффициентов, я получил ценовой диапазон для каждого дня. На графике кажется, что эта полоса диапазонов со временем расширяется, но это оптическая иллюзия: длина вертикального отрезка между красной и синей линиями в любом месте графика будет одинаковой. Теперь, когда у нас есть диапазон ценовых значений, мы можем легко получить временной диапазон, спроецировав эту полосу ценового диапазона на ось времени (с помощью обратного нелинейного уравнения). На диаграмме ниже полученный этим методом результат наглядно представлен для уровней 100 тыс. и 1 млн долларов.

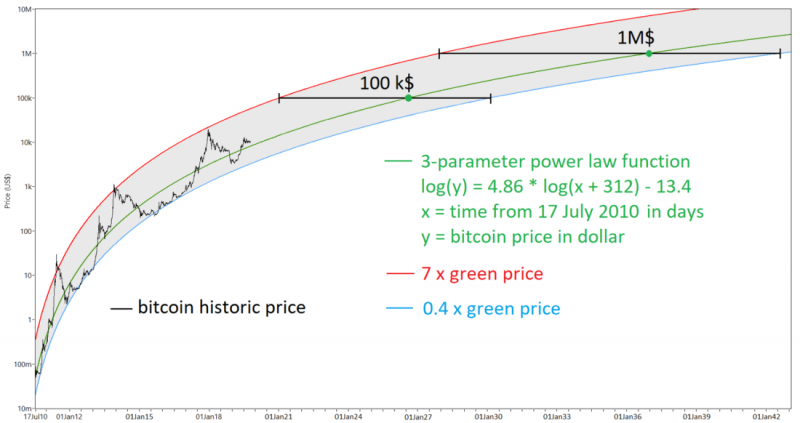
Далеко ли до Луны? Рациональные диапазоны роста биткойна

Это тот же график, что и на предыдущей картинке, только ось X продлена далеко в будущее, так что охватывает достижение смоделированным диапазоном цены биткойна 1 млн долларов. Зелёные точки – это смоделированные даты достижения биткойном 100 тыс. и 1 млн долларов, а горизонтальные отрезки – это расчётные временные диапазоны.

Этот метод возвращает следующие предполагаемые даты и временные диапазоны для достижения биткойном знаковых ценовых уровней в 100 тыс. и 1 млн $:

  • Дата достижения 100 тыс. $: 15 августа 2026 года (с 11 января 2021 до 20 февраля 2030 г.)
  • Дата достижения 1 млн $: 23 ноября 2036 года (с 30 ноября 2027 до 20 июля 2042 г.)

Эти диапазоны намного информативнее любых точечных прогнозов, потому что они генерируются строго рациональными методами, основанными на экстраполяции всего имеющегося у нас знания о цене биткойна, и с использованием уже хорошо себя зарекомендовавшей степенной модели.

Не раньше и не позже

Поскольку эта модель оценивает максимальный диапазон значений цены биткойна для каждого момента времени, она также дает следующие довольно точные подсказки:

  • До 11 января 2021 г. цена биткойна едва ли достигнет 100 тыс. $
  • До 30 ноября 2027 г. цена биткойна вряд ли достигнет 1 млн $
  • После 20 февраля 2030 г. цена биткойна, скорее всего, больше не опустится ниже 100 тыс. $
  • После 20 июля 2042 г. цена биткойна, скорее всего, больше не опустится ниже 1 млн $

Расчётные значения диапазона годового роста

Модель также можно использовать для оценки среднегодовой доходности (CAGR) сделанных сегодня инвестиций в биткойн по мере того, как цена будет следовать этим этапам:

  • CAGR при достижении 100 тыс. $: 40% (25–455 %)
  • CAGR при достижении 1 млн $: 31% (23–76%)

Расчётные результаты для 1 млн $ говорят нам, что даже при наименее крутом росте в пределах заданного диапазона среднегодовая доходность инвестиций в биткойн будет составлять 23% для периода в 22,9 лет. При реализации сценария максимального роста среднегодовая доходность составит 76% для периода в 8,3 года, в то время как при смоделированном росте среднегодовая доходность составит 31% для периода в 17,2 года.

Начало отсчёта для биткойна и валидность модели

Параметр S наилучшим образом согласуется с фактическими данными при значении 312. Мои исторические данные о цене биткойна начинаются с 17 июля 2010 г. (x=0), таким образом, S=312 соответствует 8 сентября 2009 г. (17 июля 2010 минус 312 дней) в качестве начальной даты, выбранной моделью. Это на несколько месяцев позже даты формирования генезисного блока Биткойна (3 января 2009 г.), используемой другими в своих ценовых моделях в качестве константы (вполне естественный выбор). В первые месяцы количество транзакций и адресов было очень низким, так что вряд ли можно сказать, что определение цены биткойна началось непосредственно с момента генезиса. Модель могла свободно выбирать любую дату начала, даже до генезисного блока. Тот факт, что она выбрала дату после генезиса и настолько близкую к нему, усиливает гипотезу о том, что ценовые данные биткойна действительно следуют соотношению степенного типа, что, конечно, очень трудно доказуемо и такое заключение нельзя делать только на основании линейной формы на шкале log(цена)-log(время). Иначе говоря, тот факт, что модель из трёх параметров настолько точно выбирает дату начала, повышает доверие к этой модели.

Выводы

Эти расчётные диапазоны получены путём проецирования полных доступных на сегодняшний день данных о цене биткойна в будущее с помощью трёхпараметрической степенной модели, устанавливающей метки для ориентирования в будущих изменениях цены биткойна. Притом что в самом консервативном сценарии расчётная среднегодовая доходность в долларовом эквиваленте составляет 23% за 23 года (довольно легко запомнить ;-), это представляется неплохой инвестицией. Поскольку показатели модели обновляются с каждой новой дневной точкой данных о цене биткойна, расчётные даты и темпы роста со временем будут плавно меняться. Но если биткойн продолжит вести себя так же, как в прошедшие почти десять лет, эти диапазоны должны оставаться довольно стабильными.

Добавить комментарий